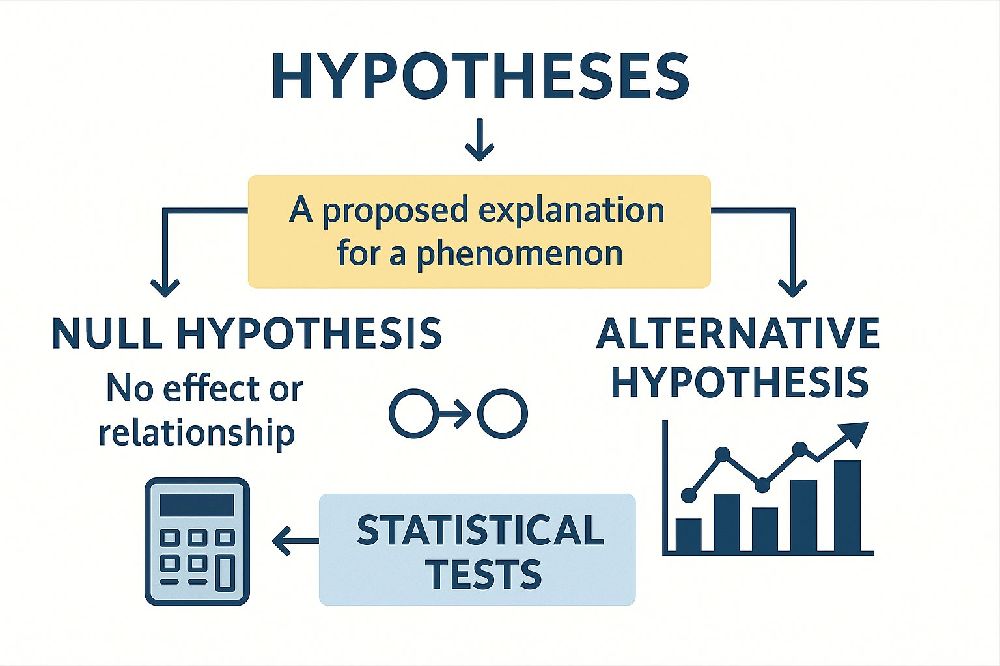
In the realm of research, a hypothesis is a statement that proposes a relationship between two or more variables.
It is a testable prediction about what will happen under certain conditions and helps guide the experimental design and research direction.
Hypotheses are foundational to the scientific method, providing a focal point for study and analysis.
They not only frame the questions researchers seek to answer but also ensure that investigations follow a logical and measurable path.

Statistical tests are used to determine the validity of a hypothesis.
These tests evaluate the data collected during research against the hypothesis, aiming to ascertain whether the observed patterns are due to chance or are statistically significant.
The choice of statistical test depends on the research design, the nature of the data, and the specific hypotheses being tested.
The outcome of these tests contributes to the broader field of inferential statistics, enabling researchers to draw meaningful conclusions about populations based on sample data, while minimizing the risk of error and bias.

Hypotheses are generally divided into two main types: the null hypothesis (H₀), which suggests no relationship or effect, and the alternative hypothesis (H₁), which proposes that a relationship or effect does exist. Through statistical testing, researchers gather evidence to either reject the null hypothesis or fail to reject it.
This process forms the backbone of inferential statistics, helping to translate raw data into meaningful scientific conclusions.

One of the critical components of hypothesis testing is determining statistical significance.
Researchers use a predefined threshold, known as the significance level (α), to decide whether the results observed are likely to have occurred by chance.
For example, an α level of 0.05 implies that there is a 5% risk of incorrectly rejecting the null hypothesis.
This balance between risk and reliability is what ensures that research findings are both accurate and credible.

Beyond statistical significance, modern research increasingly emphasizes the importance of effect size and confidence intervals.
While statistical tests indicate whether an effect is present, these additional measures help determine the magnitude and reliability of that effect.
By combining hypothesis testing with these advanced statistical tools, researchers can provide more robust, evidence-based conclusions that inform decision-making in fields such as medicine, psychology, education, and business.

Ultimately, the process of hypothesis formulation and testing is not only a cornerstone of scientific inquiry but also a safeguard against drawing erroneous conclusions.
By applying rigorous statistical methods, researchers can separate meaningful findings from random noise, thereby advancing knowledge in a way that is both systematic and verifiable.